Deep learning for the detection of γ-ray sources:
Bridging the gap between simulations and observations
with multi-modal neural networks

LISTIC, Réunion AFuTé

Author Under the supervision of
Michaël Dell'aiera (LAPP, LISTIC) Thomas Vuillaume (LAPP)
Alexandre Benoit (LISTIC)
13th June 2024
dellaiera.michael@gmail.com

Introduction

Contextualisation

**[Cherenkov Telescope Array Observatory](https://www.cta-observatory.org/)**

* Exploring the Universe at very high energies * γ-rays, powerful messenger to study the Universe * Next generation of ground-based observatories * Large-Sized Telescope-1 (LST-1) operational

**[GammaLearn](https://purl.org/gammalearn)**

* Collaboration between LAPP (CNRS) and LISTIC * Fosters innovative methods in AI for CTA * Evaluate the added value of deep learning * [Open-science](https://gitlab.in2p3.fr/gammalearn/gammalearn)

Principle of detection

Fig. Summary of the principle of detection.

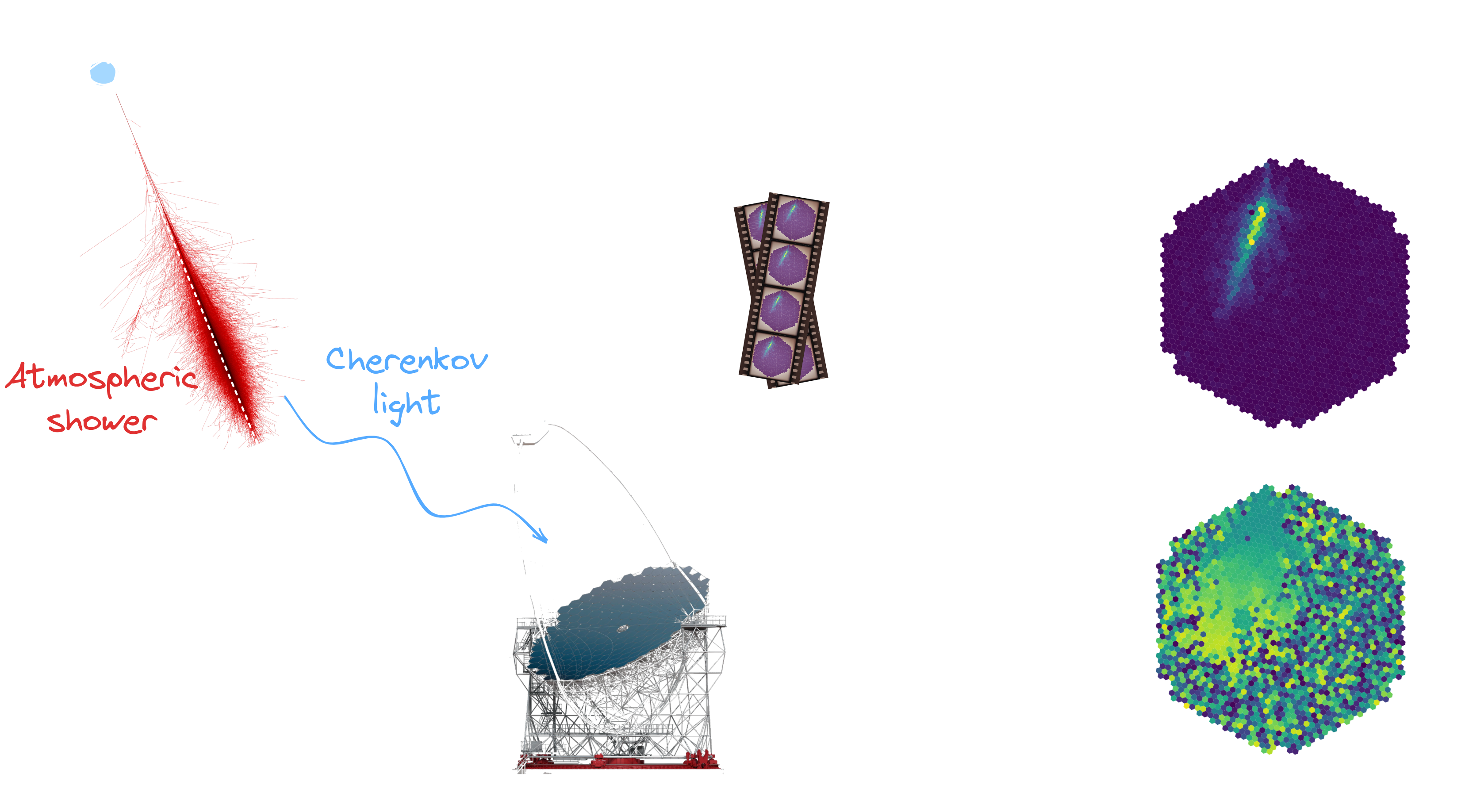
Energy flux

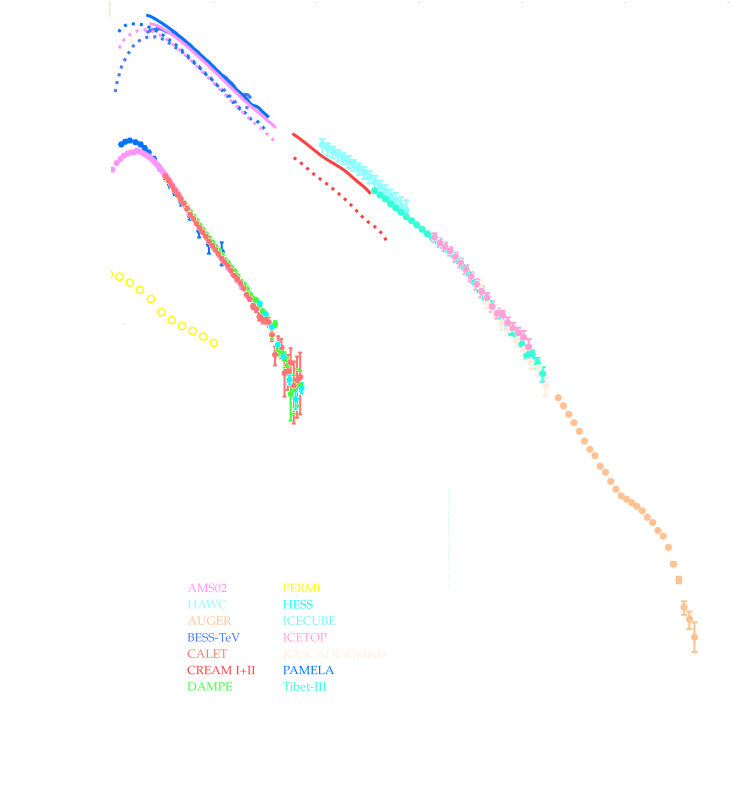
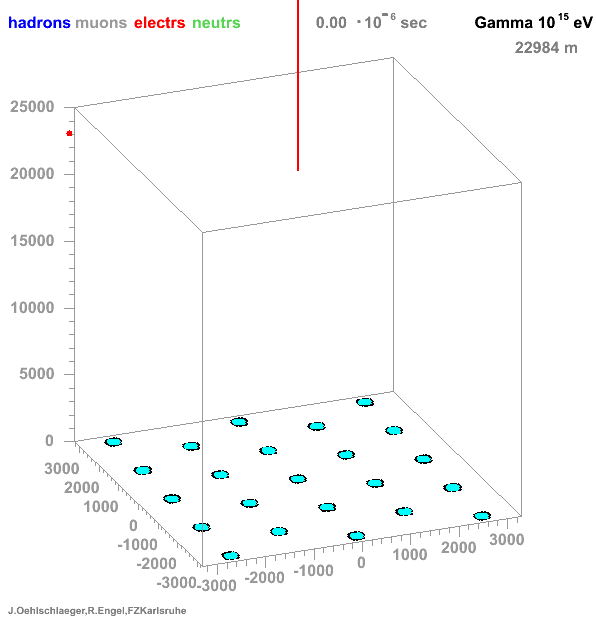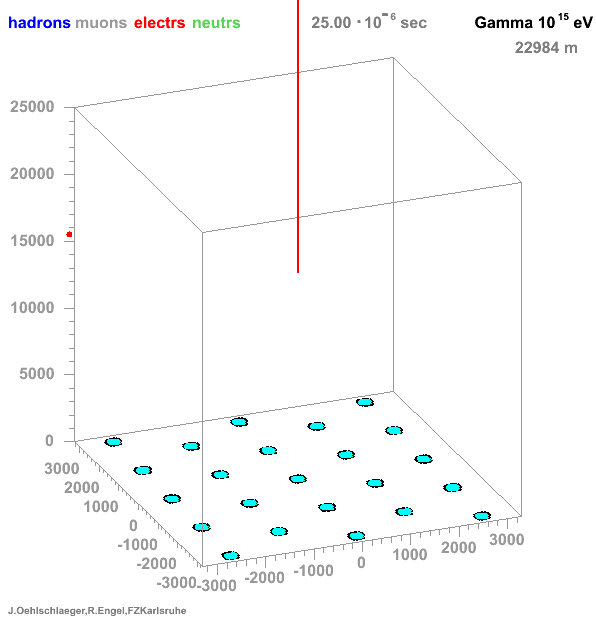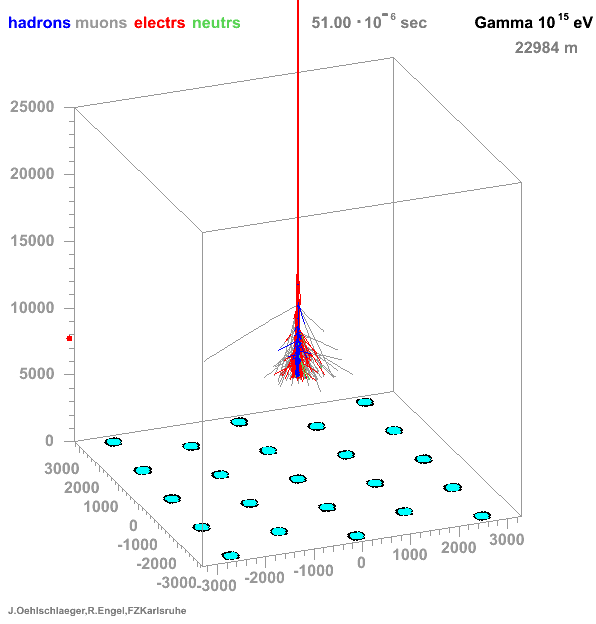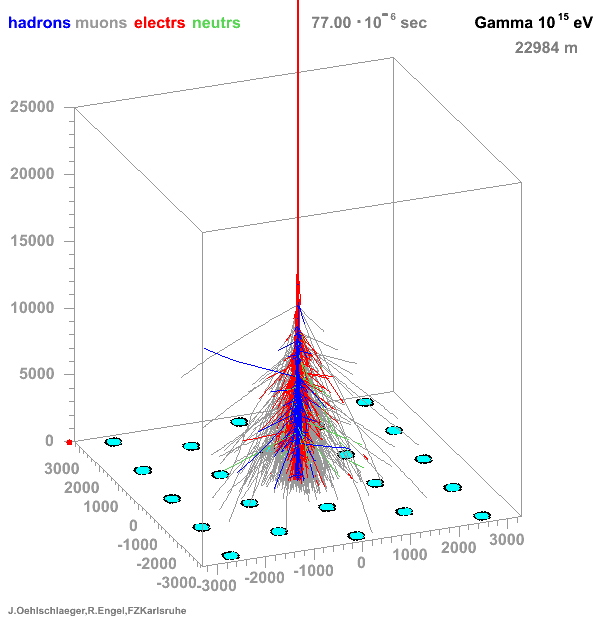
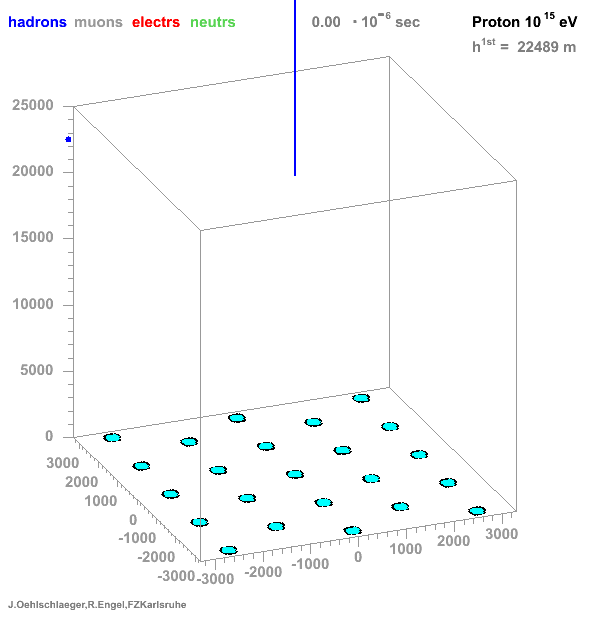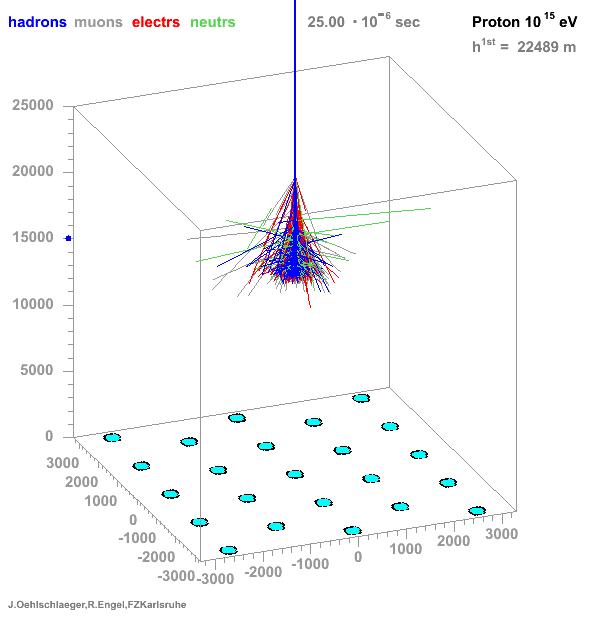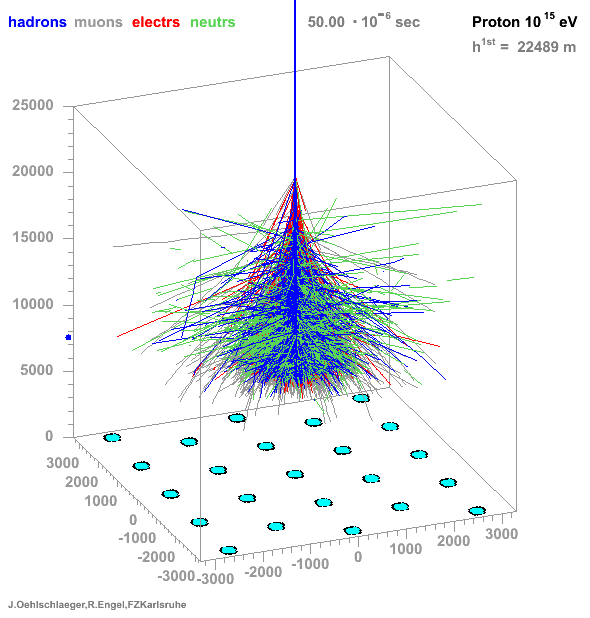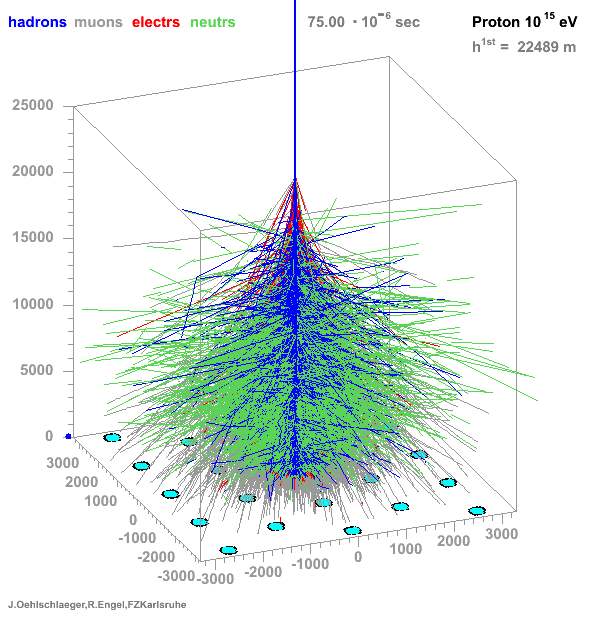
Fig. Energy flux of protons, electrons and gammas
Fig. Gamma-induced (left) and proton-induced (right) showers (CORSIKA)

* Many particles create atmospheric showers * Flux decreases with energy * Ratio gamma/proton < 1e-3

GammaLearn workflow

Fig. The detection workflow

Physical attribute reconstruction

**Real labelled data are intrinsically unobtainable**

→ Training relying on simulations (Particle shower + instrument response)

Standard analysis

* Machine learning * Morphological prior hypothesis: Ellipsoidal integrated signal * Image cleaning

GammaLearn

* Deep learning (CNN-based) * No prior hypothesis * No image cleaning

Fig. Before cleaning, after cleaning, and moments computation

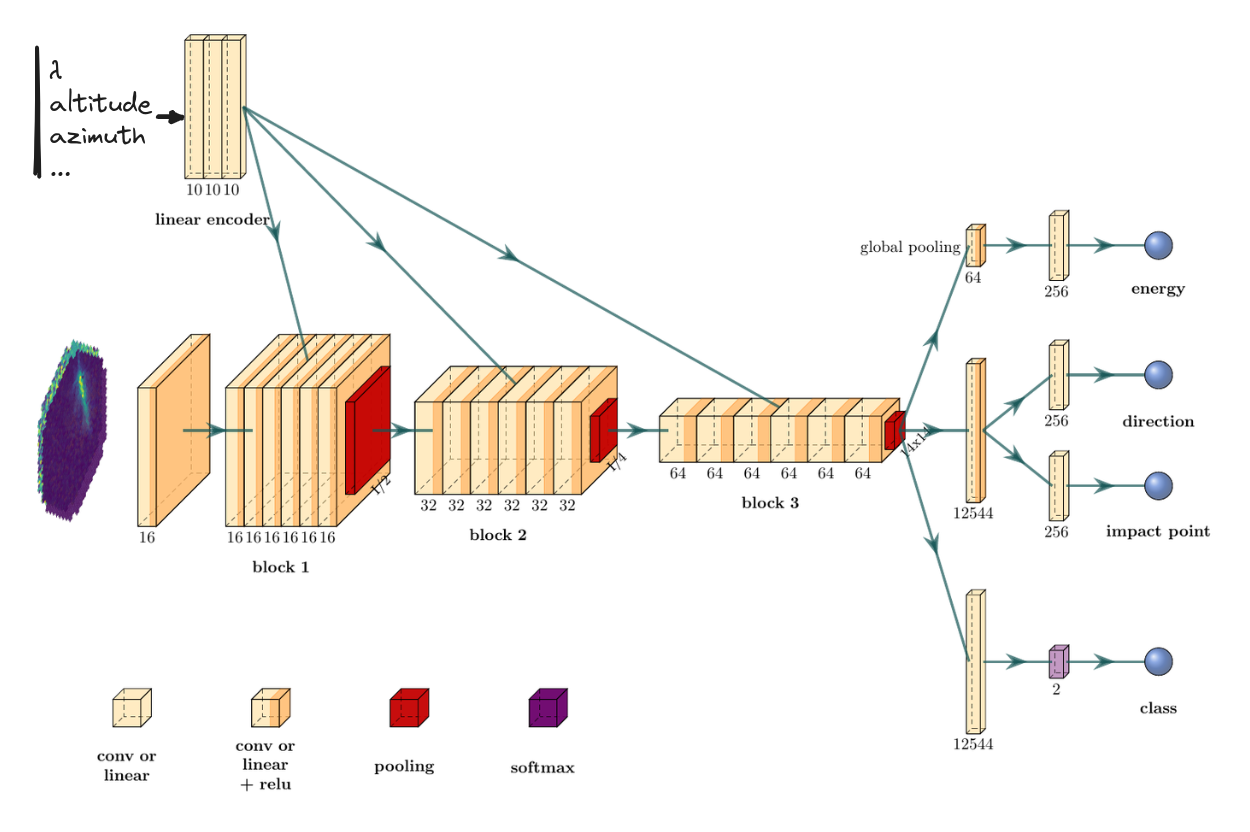
The γ-PhysNet neural network

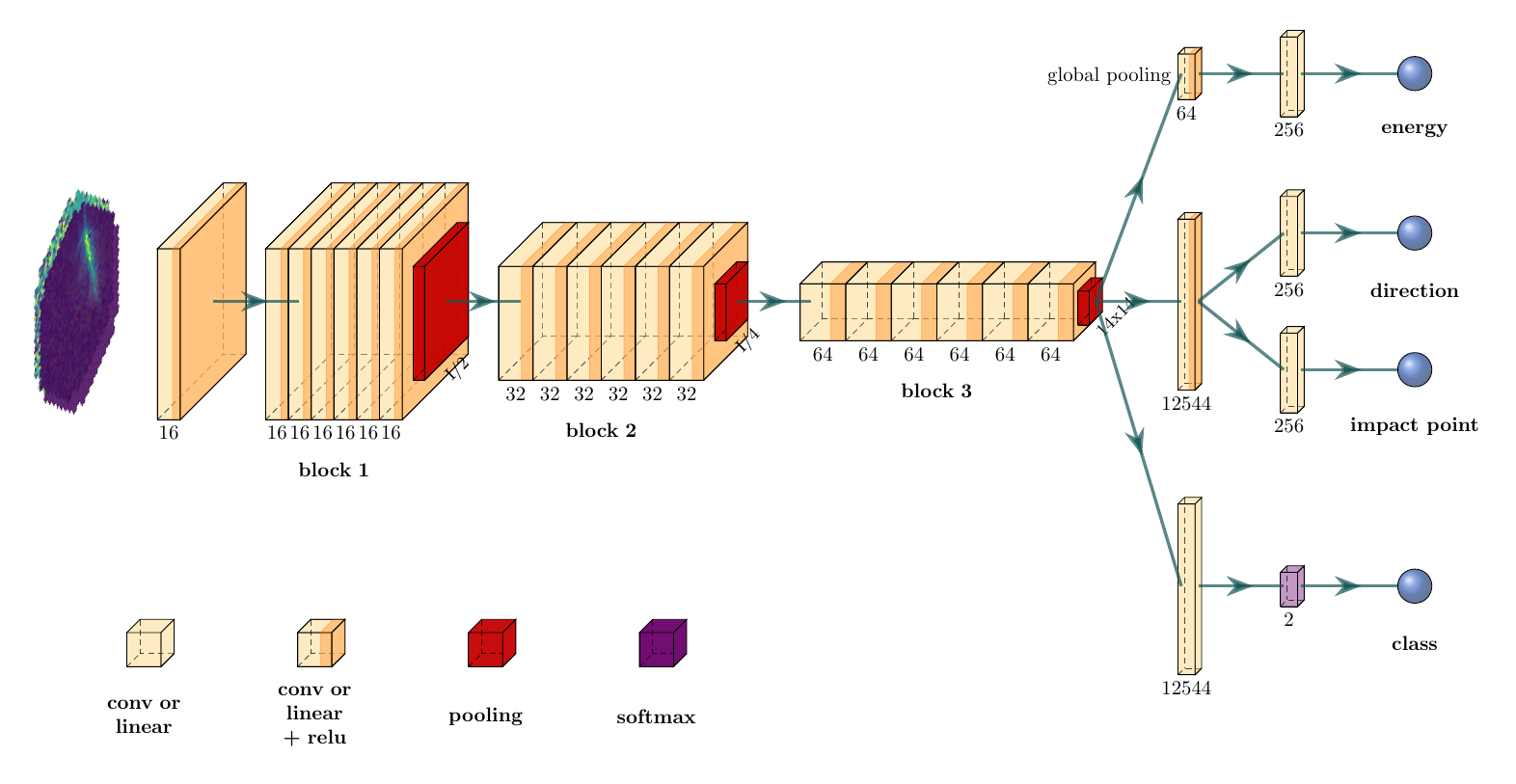
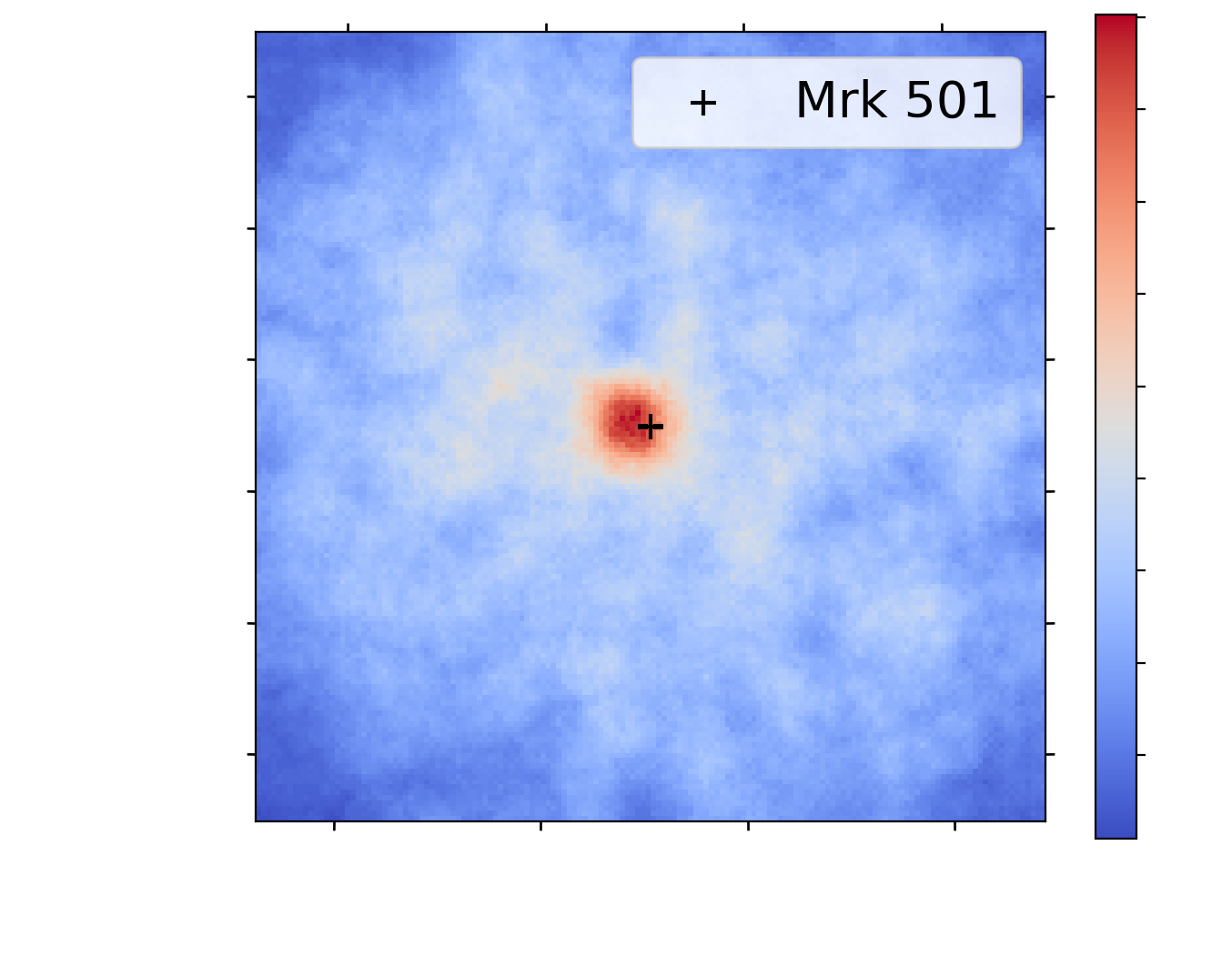
Fig. γ-PhysNet architecture (Jacquemont et al.)

Application to real data

* Capability to detect a source evaluated with significance σ = f(N_γ, N_bg) * Better results with background matching → Sensitivity to background variations → Results can be improved on telescope observations

Reconstruction algorithm Significance (higher is better) Background counts
Standard analysis + Background matching 11.9 σ 305
γ-PhysNet 12.5 σ 302
γ-PhysNet + Background matching 14.3 σ 317

Tab. Results on real data ([Vuillaume et al.](https://arxiv.org/abs/2108.04130.pdf))

The challenging transition from simulations to real data

Simulations and real data discrepencies

**Simulations are approximations of the reality**

Fig. Variation of light pollution
Fig. Stars in the FoV, dysfunctioning pixels

Simulations and real data discrepencies

Fig. Simulated pointing positions
Fig. Count map of gamma-like events around Markarian 501 (Vuillaume et al.)

Night Sky Background (NSB)

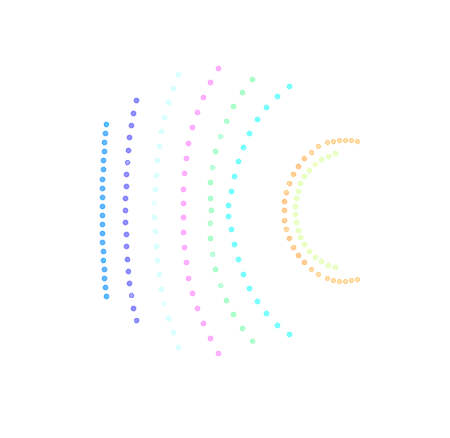
Background light from the sky: * Moonlight * Starlight * Airglow * Zodiacal light * Light pollution Main source of discreprency between simulations and real data ([Parsons et al.](https://arxiv.org/abs/2203.05315)) → Make the model robust to NSB * Data augmentation (addition of noise) noise~P(δλ) * Somehow inject the noise information within the network (δλ)

Fig. NSB distributions simulations vs real data (Vuillaume et al.)


→ Approximated by Poisson distributions

Multi-modality

Multi-modality

Normalization (pre-GPU era) * Trick to stabilize and accelerate the speed of convergence * Maintains stable gradients * Diminishes initialization influence * Allows greater learning rates

[Batch Normalization](https://arxiv.org/abs/1502.03167) (2015)

[Conditional Batch Normalization](https://proceedings.neurips.cc/paper_files/paper/2017/file/6fab6e3aa34248ec1e34a4aeedecddc8-Paper.pdf) (2017) * Elegant way to inject additional information within the network * NSB and pointing direction affects the distributions of the input data

Fig. BN vs CBN modules

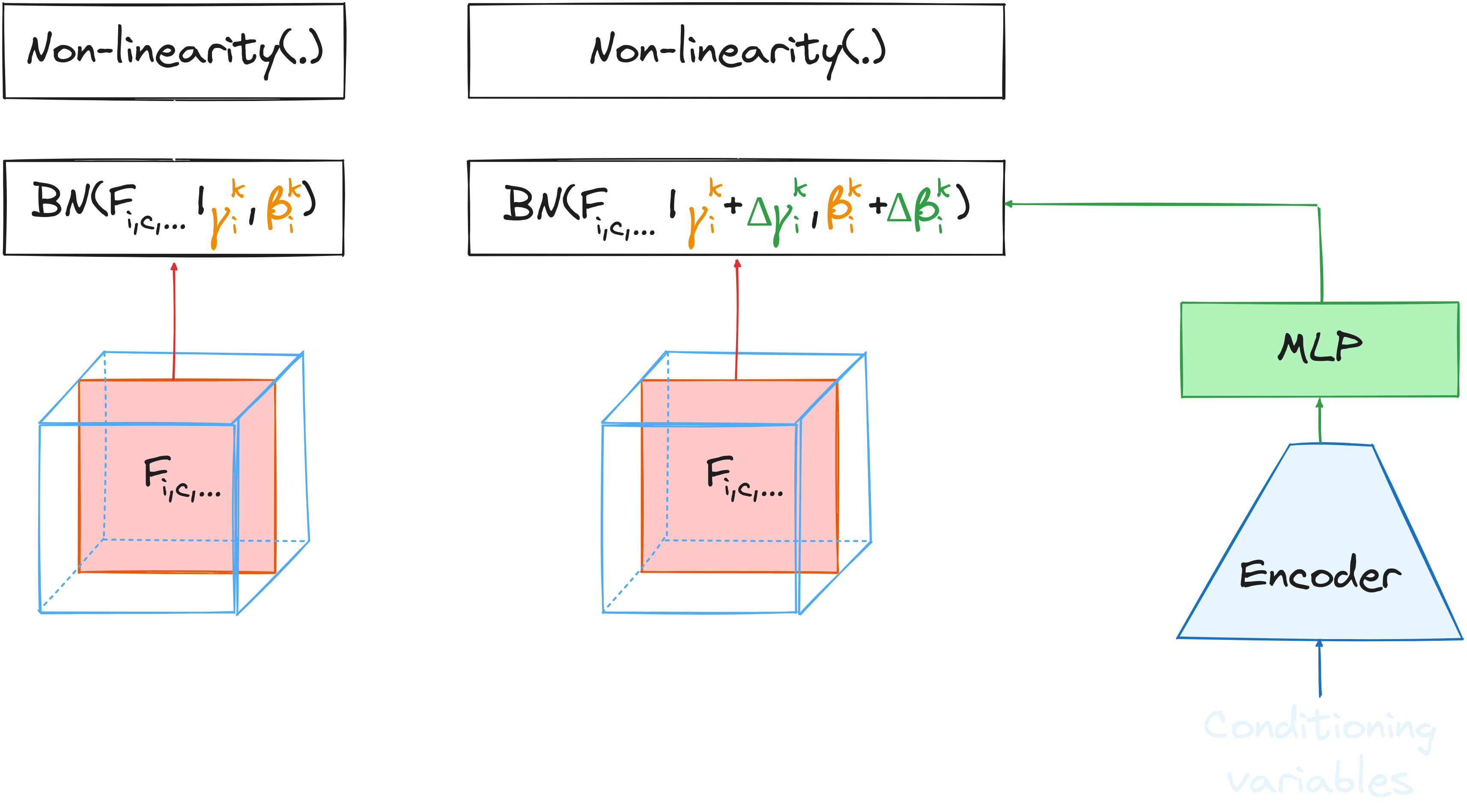
The γ-PhysNet-CBN neural network

Fig. γ-PhysNet-CBN architecture

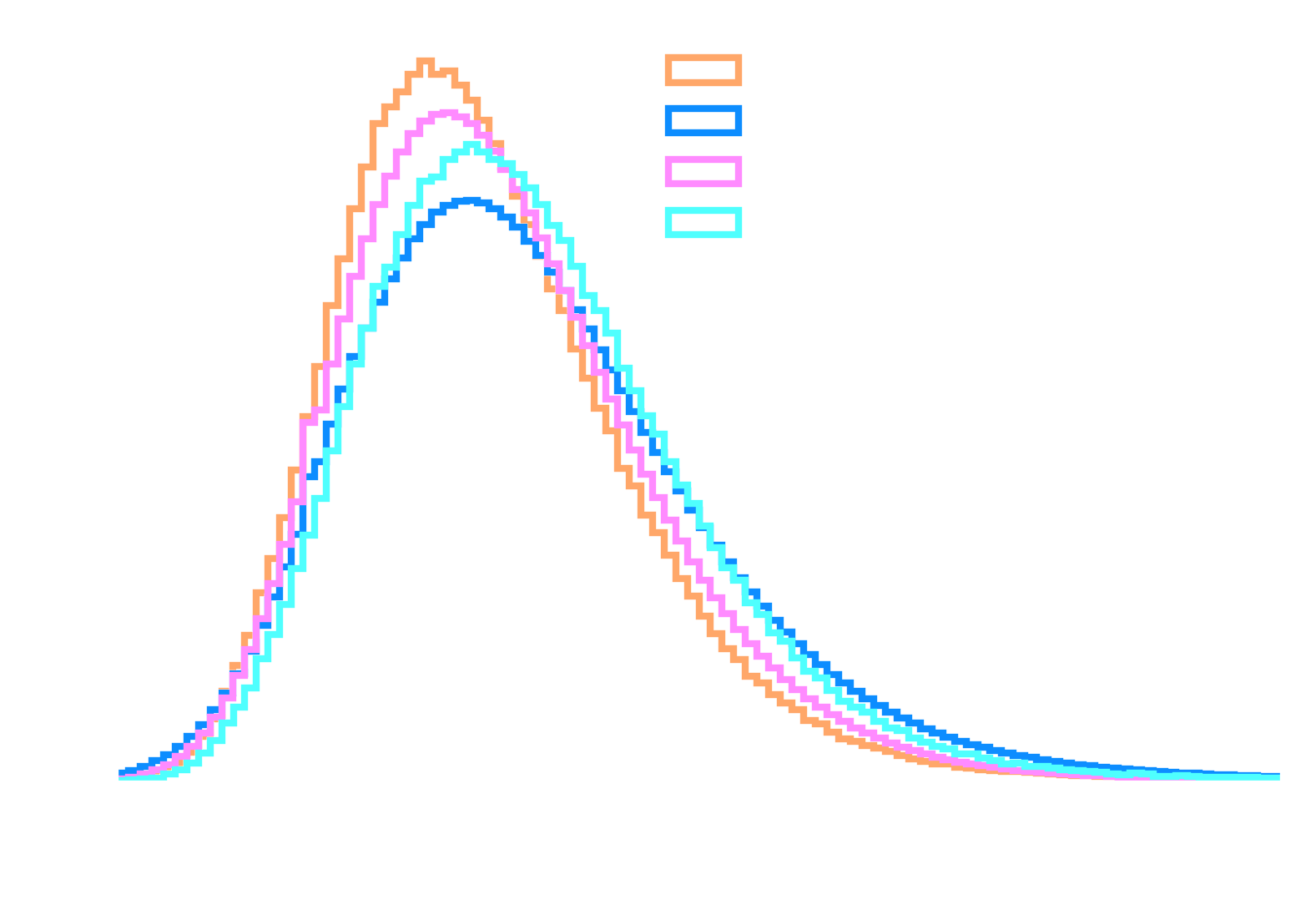
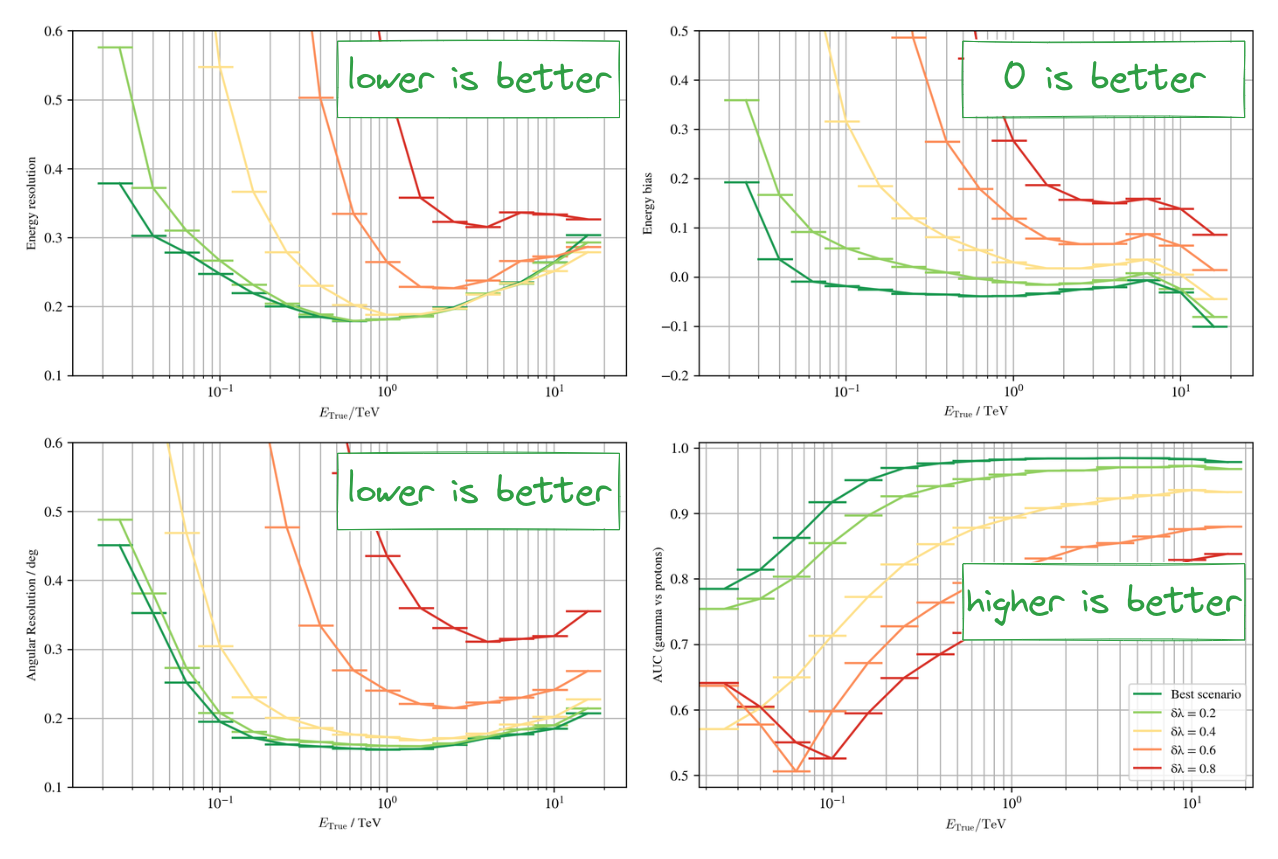
Results on simulations without CBN

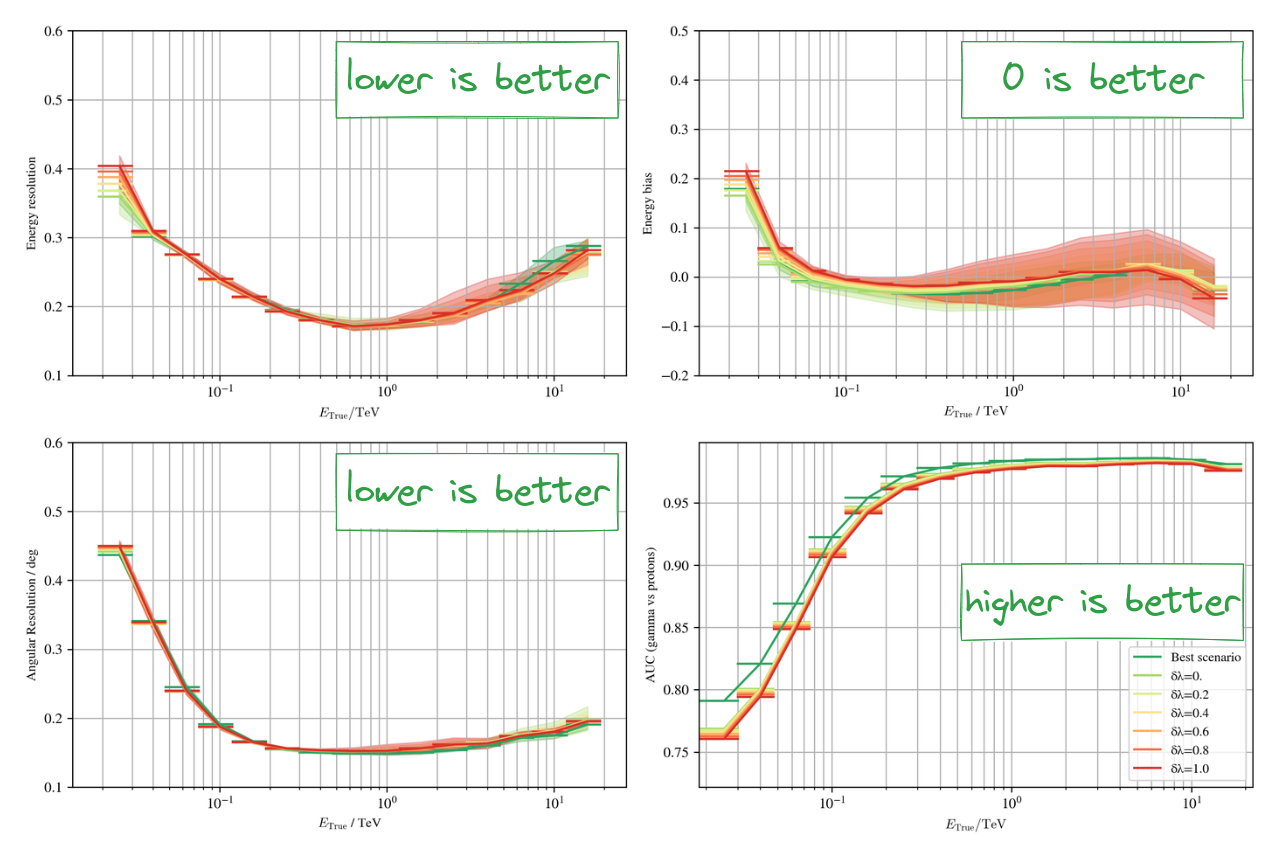
Results on simulations with CBN

Application to real data (on-going)

Pedestal images: * Signal-free acquisitions * 100 Hz acquisition rate during observations 1. Poisson approximation * Compute Poisson rate as the pixel mean * Use it as the conditioning input 2. Direct conditioning * Use the pedestals as conditioning inputs * CNN encoder * No Poisson approximation

Fig. Pedestal images

The γ-PhysNet-CBN neural network

Fig. γ-PhysNet-CBN architecture

Drawbacks of CBN

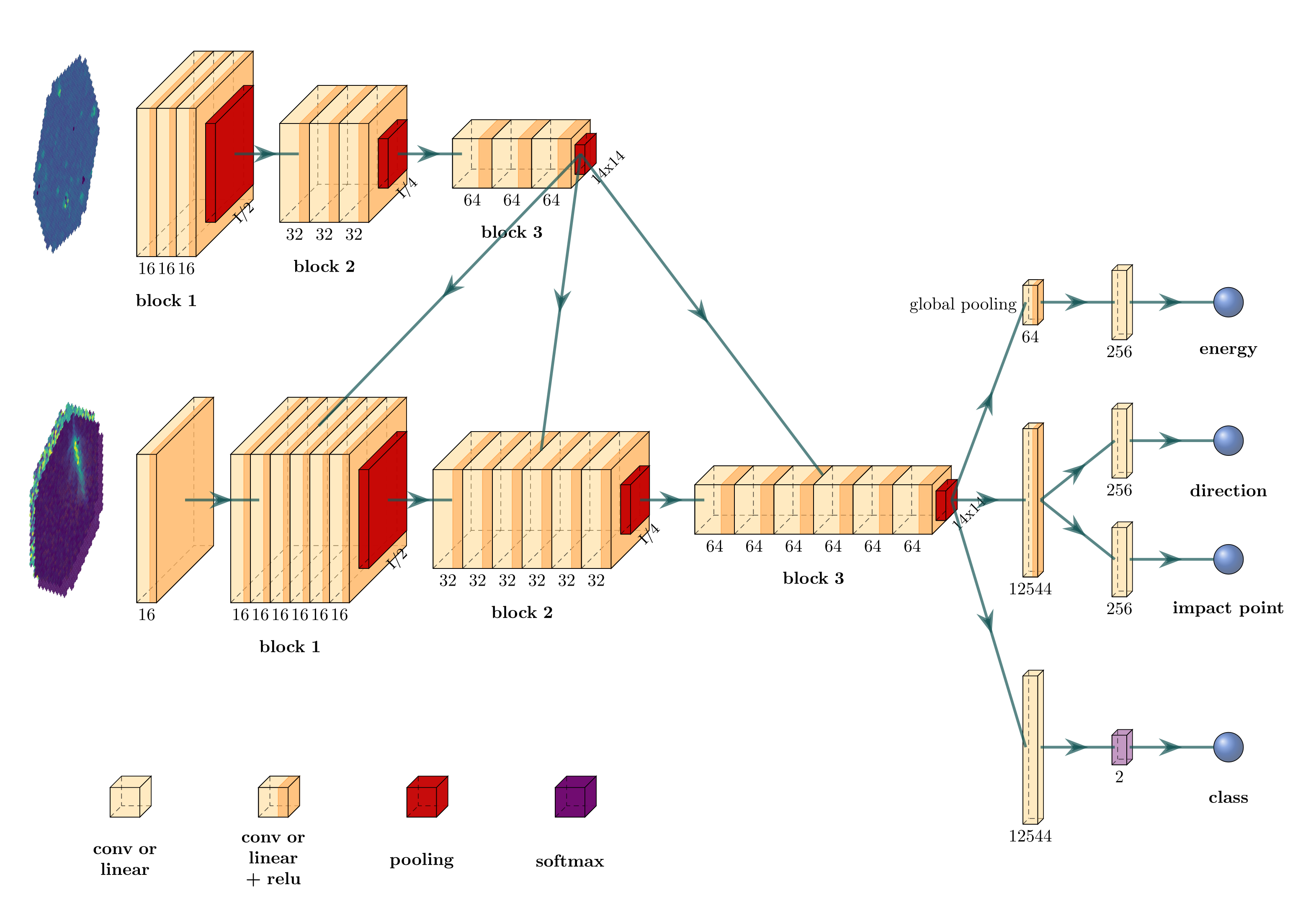
* Longer trainings are required * No miracle if information is lost

Fig. Random input data examples

Fig. Accuracies on digit classification

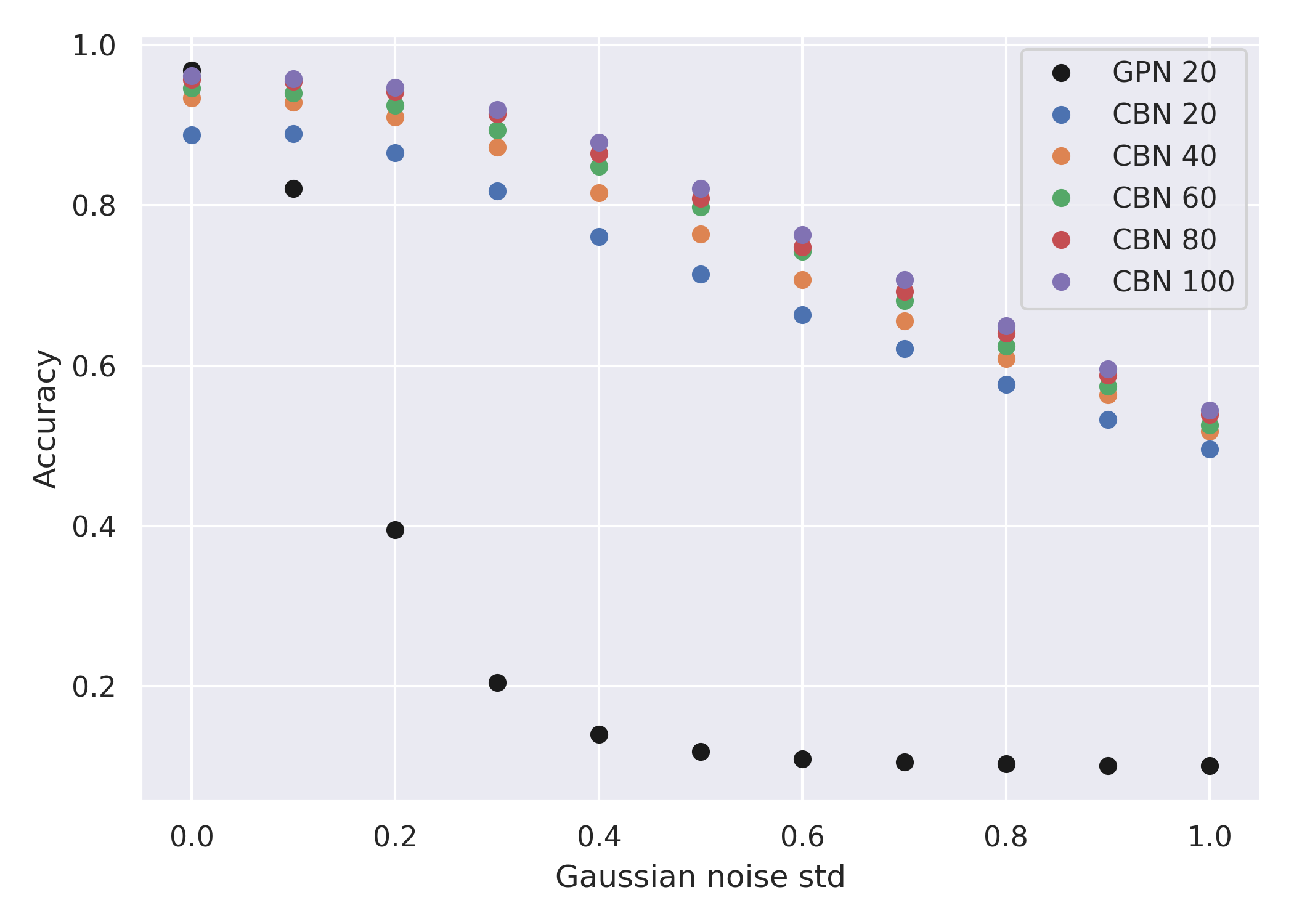
* γ-PhysNet (GPN): Trained on cleaned data, applied on noisy data * γ-PhysNet-CBN (CBN): Data augmentation

Conclusion and perspectives

Conclusion & Perspectives

  • Standard analysis and γ-PhysNet strongly affected by moonlight

  • Multi-modality (with CBN) is a novel technique to solve simulations vs real data NSB discreprency
    • Tested on simulations
    • Currently being tested on real data

  • Multi-modality increases the performance in degraded conditions

  • γ-PhysNet-CBN with pedestal image conditioning

  • Pointing direction as auxiliar conditioning inputs

  • Generalization to other sources

Acknowledgments

- This project is supported by the facilities offered by the Univ. Savoie Mont Blanc - CNRS/IN2P3 MUST computing center - This project was granted access to the HPC resources of IDRIS under the allocation 2020-AD011011577 made by GENCI - This project is supported by the computing and data processing ressources from the CNRS/IN2P3 Computing Center (Lyon - France) - We gratefully acknowledge the support of the NVIDIA Corporation with the donation of one NVIDIA P6000 GPU for this research. - We gratefully acknowledge financial support from the agencies and organizations listed [here](https://www.cta-observatory.org/consortium\_acknowledgment). - This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 653477 - This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 824064